Encryption and decryption

Encryption and decryption

symmetric Key

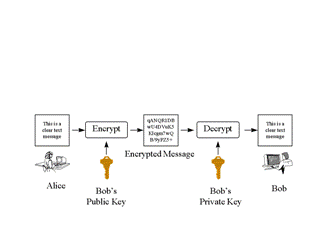
Asymatric 

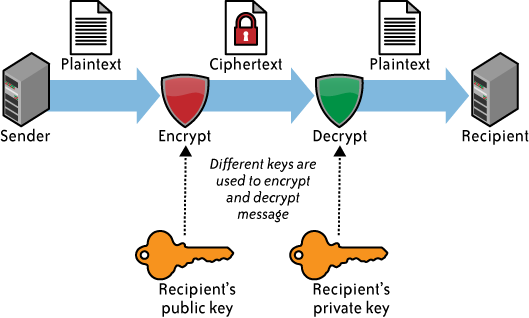
When discussing encryption, there are a few terms with which you should be familiar. The "message" is the actual data for our concern, also frequently referred to as "plain text" (denoted as "M"). Although referred to as plain text, M is not necessarily ASCII text; it might be any type of unencrypted data. It is "plain" in the sense that it does not require decryption prior to use. The encrypted message is "cipher text" (denoted as "C").

Mathematically, encryption is simply a function from the domain of M into the range of C; decryption is just the reverse function of encryption. In practice, the domain and range of most cryptography functions are the same (that is, bit or byte sequences). We denote encryption with 'C = E(M)', and decryption with 'M = D(C)'. In order for encryption and decryption to do anything useful, the equality M = D(E(M)) will automatically hold (otherwise we do not have a way of getting plain text back out of our cipher text).

Encryption and decryption, part 2

In real-life cryptography, we are not usually concerned with individual encryption and decryption functions, but rather with classes of functions indexed by a key. 'C = E{k}(M)' and 'M = D{k}(C)' denote these. For keyed functions, our corresponding automatic equality is M = D{k}(E{k}(M)). With different key indexes to our function classes, we do not expect equalities like the above (in fact, finding them would usually indicate bad algorithms): M != D{k1}(E{k2}(M)). This inequality works out nicely because all the folks without access to the key K will not know which decryption function to use in deciphering C.

The design of specific cryptographic algorithms has many details, but the basic mathematics are as simple as their portrayal in this tutorial.